权值线段树较普通线段树不同地方在于:权值线段树的数组范围 $n$ 是它的值域大小,储存的内容是这个值的出现次数。
对于数组
$$A = [1, 2, 2, 2, 3, 3, 4] $$
对应的权值线段树是
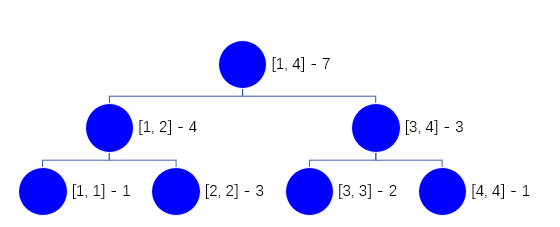
权值线段树的作用
由于权值线段树的特性,因此权值线段树可以用来实现一些普通平衡树的功能,如:
- 求某个数 $x$ 的排名
- 求排名为 $x$ 的数值
- 求某个数的前驱
- 求某个数的后继
- 插入某个数
- 删除某个数
但权值线段树也有一些弊端,因为权值线段树的数组大小是值域大小,因此当值域非常大时(如 $10^9$),需要进行离散化
插入与删除操作
权值线段树的插入与删除操作与普通线段树一致,是一种单点修改操作
inline void update(int root, int left, int right, int num, int v){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(left == right){
tree[root] += v;
return;
}
if(num <= mid)
update(lc, left, mid, num, v);
else
update(rc, mid+1, right, num, v);
tree[root] = tree[lc] + tree[rc];
}
查询第 $k$ 大元素
当左子树内权值大于等于剩余查询个数,则递归进入左子树进行查询,否则递归进入右子树进行查询。
inline int queryK(int root, int left, int right, int num){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(left == right)
return left;
if(tree[lc] >= num)
return queryK(lc, left, mid, num);
else
return queryK(rc, mid+1, right, num - tree[lc]);
}
查询 $x$ 的排名
只需要查询线段树 $[1, x-1]$ 的区间和再加上 $1$ 即可
inline int query(int root, int left, int right, int qleft, int qright){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(qleft <= left && right <= qright){
return tree[root];
}
int ans = 0;
if(qleft <= mid)
ans += query(lc, left, mid, qleft, qright);
if(qright > mid)
ans += query(rc, mid+1, right, qleft, qright);
return ans;
}
inline int rank(int x){
if(x <= 1){
return 1;
}
return query(1, 1, SIZE, 1, x-1) + 1;
}
查询前驱
当查询的数在区间的中段 $mid$ 右边时(不能相连,至少相隔1个数,否则前驱就是 $mid$,属于左子树范围),进入右子树查询,如果得到结果返回,否则进入左子树查询。
当查询节点大于右区间端点,若当前区间值为空,返回0,若右子树有值,递归进入右子树查询,否则进入左子树查询。
inline int find_pre(int root, int left, int right){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(left == right)
return left;
if(tree[rc])
return find_pre(rc, mid+1, right);
return find_pre(lc, left, mid);
}
inline int pre(int root, int left, int right, int num){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(right < num){
if(tree[root])
return find_pre(root, left, right);
return 0;
}
int ans = 0;
if(mid < num - 1 && tree[rc] && (ans = pre(rc, mid+1, right, num)))
return ans;
return pre(lc, left, mid, num);
}
查询后继
与查询前驱相反即可
inline int find_next(int root, int left, int right){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(left == right)
return left;
if(tree[lc])
return find_next(lc, left, mid);
else find_next(rc, mid+1, right);
}
inline int next(int root, int left, int right, int num){
int lc = root << 1, rc = root << 1 | 1, mid = (left + right) >> 1;
if(num < left){
if(tree[root])
return find_next(root, left, right);
return 0;
}
int ans = 0;
if(num < mid && tree[lc] && (ans = next(lc, left, mid, num)))
return ans;
return next(rc, mid+1, right, num);
}

