[图论] 求割点和桥

什么是割点和割边

在一个无向图中，如果存在一个顶点，使得删除这个顶点以后，图的联通分量增多，那么我们就称这个点是图的割点

在一个无向图中，如果存在一条边，使得删除这条边以后，图的联通分量增多，那么我们就称这条边是这个图的割边（又称桥）

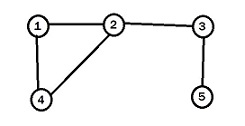
在这幅图中，节点 $2$ 和 $3$ 是割点，边 $2 – 3$ 和 $3-5$ 是割边

求解

我们通过深度优先搜索遍历这幅图，并记录下它的 $dfs$ 序，也就是时间戳，即用 $dfn$
数组保存了每个节点第一次被遍历到的时间

定义一个 $low$ 数组，表示这个点沿反向边能到达的最远祖先（这里的反向边指和 $dfs$ 方向不同的边）

如果存在一个点 $x$ 的儿子 $v$ 无法通过反向边走到这个点及其祖先上，那么这个点就是割点。

因为一个点 $v$ 如果无法从别的路径走到 $x$ 的祖先上，那么从 $x$ 的祖先走向 $v$ 的路径都必然经过点 $x$，点 $x$ 就是割点

但是需要注意 $dfs$ 的第一个节点，即使它满足上述性质，但它的儿子数量为 $1$，这个点也不是割点

如果存在一个点 $x$ 的儿子 $v$ 无法通过反向边走到这个点的祖先上，那么从 $x$ 到 $v$ 的这条边就是割边。

证明类似于割点的证明

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;
const int MAXN = 1000 + 10;
const int MAXM = 2000 + 10;

int Head[MAXN], to[MAXM], Next[MAXM], tot = 1;
int dfn[MAXN], low[MAXN], time_stamp;

int bridge_x[MAXM], bridge_y[MAXM], cnt;
int isCut[MAXN];

inline void add(int a, int b){
    to[tot] = b;
    Next[tot] = Head[a];
    Head[a] = tot++;
}

inline void addBridge(int x, int y){
    if(x > y)
        swap(x, y);

    bridge_x[cnt] = x;
    bridge_y[cnt] = y;

    cnt++;
}

inline void tarjan(int x, int fa){

    int child = 0;
    low[x] = dfn[x] = ++time_stamp;

    for(register int i=Head[x]; i; i=Next[i]){
        int v = to[i];

        if(!dfn[v]){
            child++;

            tarjan(v, x);

            low[x] = min(low[x], low[v]);

            if(low[v] >= dfn[x]){
                isCut[x] = true;
            }

            if(low[v] > dfn[x]){
                addBridge(x, v);
            }
        }

        else if(dfn[v] < dfn[x] && v != fa){
            low[x] = min(low[x], dfn[v]);
        }
    }

    if(fa == 0 && child == 1){
        isCut[x] = 0;
    }
}