[树状数组] 树状数组及其应用

树状数组支持在O(log n)进行查询和修改的数据结构。可以查询一段区间的元素之和。

树状数组实现的功能都能使用线段树来完成，但是树状数组的代码实现比较简单，容易调试。

Contents

假设原始数组为A[]，树状数组为tree[]，满足:

tree[1] = A[1]
tree[2] = A[1] + A[2]
tree[3] = A[3]
tree[4] = A[1] + A[2] + A[3] + A[4]
tree[5] = A[5]
tree[6] = A[5] + A[6]

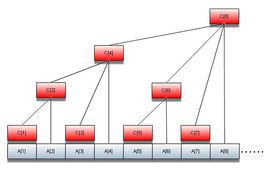
相信大家已经看出规律了，我们从另一个角度观察。

1的二进制码 : 0001
2的二进制码 : 0010
3的二进制码 : 0011
4的二进制码 : 0100
5的二进制码 : 0101
6的二进制码 : 0110

tree[i]=A[i-2^k+1]+A[i-2^k+2]+……A[i]; （k为i的二进制中从低位开始第一个1的位置） [从1开始计数]

我们引入lowbit这个概念，这段代码可以求出 $$2^k$$。

inline int lowbit(int x){
    return x & (-x);
}

求和

假设我们要求前7项
sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]
sum[7]=tree[4] + tree[6] + tree[7]
sum[7]=tree[(100)] + tree[(110)] + tree[(111)]

我么从第 $$i$$ 个位置，将tree[i]相加，同时减去 $$2^k$$

inline int sum(int i){
    int ans = 0;

    while(i){
        ans += tree[i];
        i -= lowbit(i);
    }

    return ans;

已经知道了树状数组是如何求和的，那么修改就是求和的一个逆运算

inline add(int i,int x){
    while(i<=n){ //n是树状数组的上界 
        tree[i] += x;
        i += lowbit(i);
    }
}

这些就是树状数组的实现代码