$Splay$ 是一种二叉排序树,因此满足二叉排序树的所有性质。支持在 $O(log n)$ 的时间内进行插入,删除,修改操作。
性质
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值。
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值。
(3)左、右子树也分别为二叉排序树。
(4)被查频率高的那些条目就应当经常处于靠近树根的位置(因此每次操作完后需要进行操作使其靠近树根)
实现
接下来我们所有的平衡树操作都以Luogu – 3369模板为准
旋转
$Splay$ 的复杂度保证就是依靠伸展操作,保证了树的平衡,避免其退化成为一条链。而伸展操作的本质是旋转,下面先介绍旋转操作。
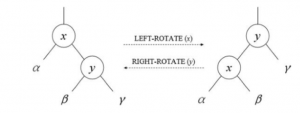
平衡树基础的旋转操作就是这两种,分别称之为左旋和右旋。
现在假设我们需要将一个节点 $x$ 通过旋转操作旋转到它的父亲节点 $f$ ,如果当前节点是父亲节点的左儿子,那么我们需要进行右旋操作;若果当前节点是父亲的右儿子,那么我们需要进行左旋操作。可以使用两个函数解决,但本人习惯通过一个 $rotate$ 函数实现这个旋转操作。
这个旋转操作可以简单的分为四个部分
- 将 $f$ 连向 $x$ 的边进行修改
- 将 $x$ 的一个儿子连向 $f$
- 更新祖父节点
- 更新大小信息
inline int getpath(int root){
return tree[fa[root]][1] == root;
}
inline void rotate(int root){
int father = fa[root];
int grandfather = fa[father];
int path = getpath(root);
tree[father][path] = tree[root][path^1];
fa[tree[father][path]] = father;
tree[root][path^1] = father;
fa[father] = root;
fa[root] = grandfather;
if(grandfather){
tree[grandfather][tree[grandfather][1] == father] = root;
}
update(father);
update(root);
}
$update$ 就是更新子树大小信息的操作。因为splay实现平衡树的常规功能,查询像第 $k$ 大,查询排名等等操作,所以需要维护一些信息。
inline void update(int root){
siz[root] = cnt[root];
siz[root] += siz[tree[root][0]];
siz[root] += siz[tree[root][1]];
}
伸展
因为每次操作完后需要进行操作使其靠近树根,所以需要不断伸展(也就是不断进行 $rotate$ 操作)
对于一个(节点,父亲,祖父)的三层同向(一条直线)的结构,需要先旋转父亲,在旋转节点,这也就是 $Splay$ 的双旋转操作。
inline void splay(int x){
for(register int f; (f = fa[x]); rotate(x)){
if(fa[f])
rotate((get(x) == get(f) ? f : x));
}
root = x;
}
前驱与后继
前驱和后继的查询和普通平衡树是一样的,前驱就是找到节点的左儿子,然后不断查找右儿子(如果存在),后继则相反
inline int Pre(){
int pos = tree[root][0];
while(tree[pos][1]){
pos = tree[pos][1];
}
return pos;
}
inline int Next(){
int pos = tree[root][1];
while(tree[pos][0]){
pos = tree[pos][0];
}
return pos;
}
插入元素
插入元素和普通平衡树操作也非常相似,不同的地方就在于有节点信息的更新和伸展操作。
inline void insert(int x){
int pos = root;
int f = 0;
if(root == 0){
tot++;
num[tot] = x;
cnt[tot] = 1;
siz[tot] = 1;
root = tot;
return;
}
while(true){
if(num[pos] == x){
cnt[pos]++;
update(pos);
splay(pos);
return;
}
f = pos;
pos = tree[pos][num[pos] < x];
if(!pos){
pos = ++tot;
cnt[pos] = 1;
num[pos] = x;
siz[pos] = 1;
fa[pos] = f;
tree[f][num[f] < x] = pos;
splay(pos);
return;
}
}
}
查询元素x的排名
从根节点开始递归,$x$ 小于当前节点向左递归,相等则返回答案,大于当前节点向右递归,排名加上左子树大小和子树根节点出现次数。
inline int rank(int x){
int pos = root;
int ans = x;
while(true){
if(tree[pos][0] && ans <= siz[tree[pos][0]]){
pos = tree[pos][0];
continue;
}
ans -= siz[tree[pos][0]];
if(ans <= cnt[pos]){
splay(pos);
return num[pos];
}
ans -= cnt[pos];
pos = tree[pos][1];
}
}
查询排名第x名的元素值
之前操作的逆过程。从 $root$ 开始递归,如果剩余可用排名小于等于左子树大小,向左递归,反之向右递归。
inline int find(int x){
int pos = root;
int ans = 0;
while(true){
if(x < num[pos]){
pos = tree[pos][0];
continue;
}
ans += siz[tree[pos][0]];
if(x == num[pos]){
splay(pos);
return ans + 1;
}
ans += cnt[pos];
pos = tree[pos][1];
}
}
删除
删除操作比较复杂。首先需要将节点旋转到根,这个可以通过 $find$ 操作解决。然后还需要对一些特殊情况进行特殊处理(根节点只有左儿子或者右儿子,或者根节点出现次数不止一次),对于常规情况,我们将删除节点的前驱作为新的根,然后更新相关信息即可。
inline void Delete(int x){
find(x);
if(cnt[root] > 1){
cnt[root] --;
update(root);
return;
}
if(!tree[root][0] && !tree[root][1]){
clear(root);
root = 0;
return;
}
if(!tree[root][0] && tree[root][1]){
int oldroot = root;
fa[tree[root][1]] = 0;
root = tree[root][1];
clear(oldroot);
return;
}
if(tree[root][0] && !tree[root][1]){
int oldroot = root;
fa[tree[root][0]] = 0;
root = tree[root][0];
clear(oldroot);
return;
}
int Left = Pre();
int oldroot = root;
splay(Left);
fa[tree[oldroot][1]] = root;
tree[root][1] = tree[oldroot][1];
clear(oldroot);
update(root);
return;
}
说明
以上还只是 $Splay$ 实现一棵平衡树的基本操作,$Splay$ 还能够处理区间问题(区间求和,区间修改,区间翻转等),还可以作为一些数据结构的一部分( $LCT$ ,树套树),同时 $Splay$ 还有分裂与合并等操作,这些都会在接下来的文章中介绍到。

