简介
快速离散傅里叶变换是计算离散傅里叶变换以及其逆变换的快速算法。按照 $DFT $ 的定义计算一个长度为 $n $ 的序列的 $DFT $ 需要的时间复杂度为 $O(n^2) $,而 $FFT $ 的时间复杂度仅为 $O(n \ log\ n) $
$FFT $ 在 OI 中的重要运用是可以在 $O (n \ log \ n) $ 的时间内求出两个多项式 $F(x) $ 和 $G(x) $ 的卷积
朴素的多项式乘法
令两个多项式 $F(x) = \sum_{i=0}^{n-1}a_ix^i $ , $G(x) = \sum_{i=0}^{n-1}b_ix^i $
我们要求出 $H(x) = F(x) \times G(x)$
$$ H(x) = \sum_{k=0}^{2n-2}(\sum_{k=i+j}a_ib_j)x^k $$
非常显然,这样的朴素的多项式乘法是 $O(n^2) $的,效率非常低下
在学习 $FFT $ 之前,我们先了解几个定义
多项式的表示
既然 $FFT $ 主要用于多项式 卷积运算 ,我们先来了解如何表示一个多项式
系数表示法
在一个关于变量 $x $ 的多项式 $F(x) $ 中,$x_k $ 的系数一般用下标 $k $ 标记。
$$ F(x) = a_k x^k + a_{k-1} x^{k-1} + \cdots + a_1 x^1 + a_0 $$
这个多项式是由一个 $n $ 唯向量 $(a_0, a_1, \cdots, a_k) $ 唯一确定 的,这是最常用的一种多项式的表示方式
点值表示法
我们将多项式 $F(x) $ 看做一个 $n $ 次函数,我们在函数上选取 $n+1 $ 个点,这 $n+1 $ 个点即可 唯一确定 这个多项式 $F(x) $
你可以将这 $n+1 $ 个确定的点代入多项式 $F(x)$ 中
$$
\begin{cases}
F(x_0) = y_0 = a_0 + a_1x_0 + a_2 x_0^2 + \cdots + a_n x_0^n & \\
F(x_1) = y_1 = a_0 + a_1x_1 + a_2 x_1^2 + \cdots + a_nx_1^n & \\
\cdots & \\
F(x_n) = y_n = a_0 + a_1x_n + a_2x_n^2 + \cdots + a_n x_n^n &
\end{cases}
$$
通过高斯消元法,这 $n+1 $ 个未知的系数向量 $(a_0, a_1, \cdots, a_n) $ 可以被唯一确定
而离散傅里叶变换 $DFT $ 就是将多项式从 系数表达式 转化为 点值表达式 的过程
逆离散傅里叶变换 $IDFT $ 就是将多项式从 点值表达式 转换回 系数表达式 的过程
复数
复数的定义
复数域是实数域的一个延伸,它使得任何一个多项式方程都有根。复数中有一个 虚数单位 $i $,它是 $-1 $ 的平方根,即 $i^2 = -1 $,任一复数都可表达为 $x + yi $,其中 $x $ 和 $y $ 均为实数,分别称为复数的 实部 和 虚部
复平面的定义
在复平面中, $x $ 轴代表 实部,$y $ 轴代表 虚部
任何一个复数 $a + bi $ 都可以对应复平面上一个从 $(0, 0) $ 指向 $(a, b) $ 的向量
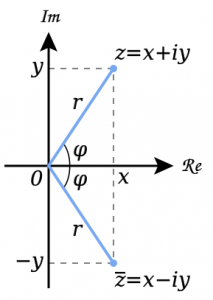
这个向量的长度 $\sqrt{a^2+b^2} $ 叫做模长,$x $ 轴正半轴到该向量的的有向角叫做幅角
复数的相加遵循 平面四边形法则,复数相乘时 模长相乘 幅角相加
单位复根
数学上,$n $ 次单位复根是 $n $ 次幂为 $1 $ 的复数,它们位于复平面的单位圆上,一共有 $n $ 个。
其中,我们将 最小的幅角为正 的向量对应的复数称作 $n $ 次 主单位复根,简记为 $\omega_n $
其余各单位复根可以表示为 $\omega_n^0, \omega_n^1 , \cdots, \omega_n^n $,其中 $\omega_n^0 = \omega_n^n = 1 $
我们可以求出 $\omega_n^k $ 的幅角,因此可以得到它的表达式
$$ \omega_n^k = cos \ k \frac{2 \pi}{n} + sin \ k \frac{2 \pi}{n} i $$
单位复根的性质
性质1 : $\omega_{2n}^{2k} = \omega_{n}^{k} $
性质2 : $\omega_{n}^{k+\frac{n}{2}} = -\omega_n^k$
性质1直接用单位复根的三角表达式代入证明即可,下面证明一下性质2
$$
\begin{equation}
\begin{aligned}
\omega_{n}^{k+\frac{n}{2}} & = \omega_n^k \times \omega_n^{\frac{n}{2}} \\
& = \omega_n^k \times (cos \ n \frac{2 \pi}{2n} + sin \ n \frac{2 \pi}{2n} i) \\
& = \omega_n^k \times (cos \ \pi + sin\ \pi \ i) \\
& = -\omega_n^k
\end{aligned}
\end{equation}
$$
离散傅里叶变换 DFT
对于接下来所有出现的 $n $ 均视为 $2 $ 的正整数次幂
对于 $n-1 $ 次多项式 $f(x) $,我们将 $n $ 次单位复根 代入多项式 $f(x) $,得到的点值向量 $(f(\omega_{n}^0), f(\omega_{n}^1), \cdots, f(\omega_{n}^n)) $ 称为 $(a_0, a_1, \cdots, a_{n-1}) $ 的离散傅里叶变换
考虑通过 奇偶划分 的分治方法进行离散傅里叶变换,时间复杂度 $O(n \ log \ n) $
$$ f(x) = (a_0 + a_2 x^2 + \cdots + a_{n-2} x^{n-2}) + (a_1x + a_3 x^3 + \cdots + a_{n-1}x^{n-1}) $$
$$f_1(x) = a_0 + a_2 x + \cdots + a^{\frac{n}{2}-1} $$
$$f_2(x) = a_1 + a_3 x + \cdots + a^{\frac{n}{2}-1} $$
$$f(x) = f_1(x^2) \times x f_2(x^2) $$
对于 $k < \frac{n}{2} $
$$\begin{equation}
\begin{aligned}
f(\omega_{n}^{k}) & = f_1(\omega_{n}^{2k}) + \omega_n^k f_2(\omega_{n}^{2k}) \\
& = f_1(\omega_{\frac{n}{2}}^k) + \omega_{n}^{k} f_2(\omega^{k}_{\frac{n}{2}})
\end{aligned}
\end{equation}
$$
$$\begin{equation}
\begin{aligned}
f(\omega_{n}^{k+\frac{n}{2}}) & = f_1(\omega_n^{2k} \times \omega_{n}^{n}) + \omega_{n}^{k+\frac{n}{2}} f_2(\omega_{n}^{2k} \times \omega_{n}^{n}) \\
& = f_1(\omega_{\frac{n}{2}}^k) – \omega_{n}^{k} f_2(\omega^{k}_{\frac{n}{2}})
\end{aligned}
\end{equation}
$$
那么我们便可将问题不断递归下去,每当知道了 $f_1(x) $ 和 $f_2(x) $ 在 $\omega_{\frac{n}{2}} $处的所有点值,便可在 $O(n) $ 时间内得到 $f(x) $ 在 $\omega_{n} $ 处的所有点值
递归层数最多为 $log \ n $ 层,时间复杂度 $O(n \ log \ n) $
蝴蝶变换
但是递归实现的 $FFT $ 常数还是非常大,我们一般通过 蝴蝶操作 迭代地进行傅里叶变换
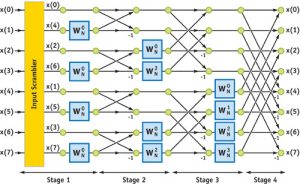
上面是一个 $8$ 基 $DFT$ 蝴蝶变换的示意图
之前我们已经通过递归的方式实现了 $DFT$,我们模拟一下递归过程
0 1 2 3 4 5 6 7
0 2 4 6 1 3 5 7
0 4 2 6 1 5 3 7
我们将起始位置二进制码和最终位置二进制码进行比较
0 : 000 -> 000 [0]
1 : 001 -> 100 [4]
2 : 010 -> 010 [2]
3 : 011 -> 110 [7]
4 : 100 -> 001 [1]
5 : 101 -> 101 [5]
6 : 110 -> 011 [3]
7 : 111 -> 111 [7]
发现实际上是 二进制位翻转 得到的结果,那么我们就得到了每一个 初始位置 在递归到 最底层时的位置
int k = 0;
while((1 << k) < n)
k++;
for(register int i=0; i<n; i++){
for(register int j=0; j<k; j++){
if(i & (1 << j))
place[i] |= (1 << (k - j - 1));
}
}
状态合并
下面考虑如何合并两个状态
$a(k)$ 保存了 $f_1(\omega_{\frac{n}{2}}^k) $的答案,$a(\frac{n}{2} + k)$ 保存了 $f_2(\omega_{\frac{n}{2}}^k) $的答案
我们用一个变量 $t$ 储存 $\omega_{n}^{k} \times f_2(\omega_{\frac{n}{2}}^k)$ 的答案
$$ a(\frac{n}{2} + k) = a(k) \ – \ t $$
$$ a(k) = a(k) + t $$
这就是 $DFT$ 的蝴蝶操作
complex 是一个存储复数的变量类型
omega[k] 储存 $\omega_n^k$,当长度为 $l$ 时,$\omega_{l}^k = \omega_{n}^{\frac{n}{l}k} $
我们先枚举区间长度 $range$,计算出分治点 $mid$,然后模拟划分一段段的储存答案的 $p$,通过蝴蝶操作合并
for(register int range=2; range <=n; range <<= 1){
int mid = range >> 1;
int k = n / range;
for(register complex *p = a; p != a + n; p += range){
for(register int i=0; i<mid; i++){
int tmp = mid + i;
complex t = omega[k * i] * p[tmp];
p[tmp] = p[i] - t;
p[i] = p[i] + t;
}
}
}
离散傅里叶逆变换 IDFT
假设多项式 $f(x)$ 通过 $DFT$ 变换得到了一个 $n$ 维点值向量 ($y_0, y_1, \cdots, y_{n-1}$),其原系数向量为 ($c_0, c_1, \cdots, c_{n-1}$)
$$y_k = \sum_{i=0}^{n-1} c_i (\omega_n^k)^i $$
$$
\begin{equation}
\begin{aligned}
c_k & = \frac{1}{n} \sum_{i=0}^{n-1} y_i(\omega_n^{-k})^i \\
& = \frac{1}{n} \sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}c_j(\omega_n^i)^j)(\omega_n^{-k})^i \\
& = \frac{1}{n} \sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}c_j(\omega_n^j)^i)(\omega_n^{-k})^i \\
& = \frac{1}{n} \sum_{i=0}^{n-1} (\sum_{j=0}^{n-1}c_j(\omega_n^j)^i (\omega_n^{-k})^ i) \\
& = \frac{1}{n} \sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}c_j (\omega_n^{j-k})^i) \\
& = \frac{1}{n} \sum_{i=0}^{n-1} \sum_{j=0}^{n-1} c_j (\omega_n^{j-k})^i \\
& = \frac{1}{n} \sum_{j=0}^{n-1} a_j(\sum_{i=0}^{n-1}(\omega_n^{j-k})^i)
\end{aligned}
\end{equation}
$$
我们发现 $$1 + \omega_n^k + (\omega_n^k)^2 + \cdots + (\omega_n^k)^{n-1} = \frac{1-(\omega_n^k)^n}{1-\omega_n^k}$$
当 $k \not = 0 $时,$\sum_{i=0}^{n-1} (\omega_n^k)^i = 0$,否则值为 $n$
所以
$$c_i = \frac{1}{n} y_i $$
$IDFT$的过程就是用单位根的倒数替代单位根,再做一次 $DFT$ 变换,最后将结果除以 $n$即可得到答案
单位根的倒数即为它的 共轭复数,可以使用 complex 库的 conj() 求得
模板
考虑到 C++ 的 complex 效率不高,我们可以手写 complex 运算
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int MAXN = 2097152 + 10;
const double PI = acos(-1.0);
// complex 定义
struct complex{
double x, y;
complex (double xx=0, double yy=0){x=xx, y=yy;}
};
complex operator + (complex a, complex b){return complex(a.x+b.x, a.y + b.y);}
complex operator - (complex a, complex b){return complex(a.x-b.x, a.y - b.y);}
complex operator * (complex a, complex b){return complex(a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x);}
//储存单位根,共轭复数
complex omega[MAXN], omegaInverse[MAXN];
int place[MAXN];
inline void init(int n){
//二进制翻转预处理
int k = 0;
while((1 << k) < n)
k++;
for(register int i=0; i<n; i++){
for(register int j=0; j<k; j++){
if(i & (1 << j))
place[i] |= (1 << (k - j - 1));
}
}
//单位根预处理
double single = 2 * PI / n;
for(register int i=0; i<n; i++){
omega[i] = complex(cos(single*i), sin(single*i));
omegaInverse[i] = complex(omega[i].x, -omega[i].y);
}
}
inline void transform(complex *a, int n, complex *omega){
//交换位置
for(register int i=0; i<n; i++){
if(i < place[i])
swap(a[i], a[place[i]]);
}
//蝴蝶操作
for(register int range=2; range <=n; range <<= 1){
int mid = range >> 1;
int k = n / range;
for(register complex *p = a; p != a + n; p += range){
for(register int i=0; i<mid; i++){
int tmp = mid + i;
complex t = omega[k * i] * p[tmp];
p[tmp] = p[i] - t;
p[i] = p[i] + t;
}
}
}
}
inline int read(){
int x = 0;
char ch = getchar();
while(ch < '0' || ch > '9')
ch = getchar();
while('0' <= ch && ch <= '9'){
x = x*10 + ch - '0';
ch = getchar();
}
return x;
}
int n1, n2;
complex c1[MAXN], c2[MAXN];
int ans[MAXN];
int main(){
n1 = read();
n2 = read();
n1++;
n2++;
int n = 1;
//n需为2的正整次幂
while(n < n1 + n2)
n <<= 1;
for(register int i=0; i<n1; i++)
c1[i].x = read();
for(register int i=0; i<n2; i++)
c2[i].x = read();
init(n);
//DFT
transform(c1, n, omega);
transform(c2, n, omega);
//进行多项式乘法运算
for(register int i=0; i<n; ++i)
c1[i] = c1[i] * c2[i];
//IDFT
transform(c1, n, omegaInverse);
//输出结果
for(register int i=0; i<n1+n2-1; i++){
printf("%d ", (int)floor(c1[i].x/n + 0.5));
}
return 0;
}

