[题解] LOJ – 10149 凸多边形的划分

题目描述

给定一个具有 $N$ 个顶点的凸多边形，将顶点从 $1$ 至 $N$ 标号，每个顶点的权值都是一个正整数。将这个凸多边形划分成 $N-2$ 个互不相交的三角形，试求这些三角形顶点的权值乘积和至少为多少。

输入格式

输入第一行为顶点数 $N$
第二行依次为顶点 $1$ 至顶点 $N$ 的权值。

输出格式

输出仅一行，为这些三角形顶点的权值乘积和的最小值

输入样例

5
121 122 123 245 231

输出样例

12214884

##数据范围及提示
对于 $100 \%$ 的数据，有 $N \leq 50$，每个点权值小于 $10^9$

时空限制

时间限制：1s
空间限制：512MB

解题思路

考虑区间 $DP$，我们先将顶点按顺时针顺序从任意顶点开始编号为 $1, 2, \cdots, n$

令数组 $f[l][r]$ 表示顶点编号为 $l, l+1 , \cdots, r$ 的凸多边形权值乘积和最小值

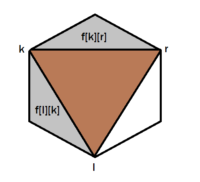
一个凸多边形可以由两个小的凸多边形和两个小凸多边形中间空隙构成的三角形组成

$$f[l][r] = min(f[l][k] + f[k][r] + a_l \times a_r \times a_k)$$

其中

$$l+1 \leq k \leq r-1 $$

显然，这道题还需要进行高精度运算

代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;
const int SIZE = 35 + 10;
const int MAXN = 50 + 10;

struct bigNum{
    int len;
    int data[SIZE]; 

    bigNum(char *_input){
        memset(data, 0, sizeof(data));

        len = strlen(_input);

        for(register int i=0; i<len; i++)
            data[i] = _input[len-i-1] - '0';            
    }

    bigNum(){
        memset(data, 0, sizeof(data));
        len = 0;
    }

    bool operator < (bigNum const a) const{
        if(len < a.len)
            return 1;
        if(len > a.len)
            return 0;

        for(register int i=len-1; i>=0; i--){
            if(data[i] < a.data[i])
                return 1;
            else if(data[i] > a.data[i])
                return 0;
        }

        return 0;
    }

    bool operator == (bigNum const a) const{
        if(len != a.len)
            return 0;

        if(memcmp(data, a.data, sizeof(data)) == 0)
            return 1;

        return 0;
    }

    void print(){
        for(register int i=len-1; i>=0; i--)
            printf("%d", data[i]);
    }


    bigNum operator + (bigNum const a){
        bigNum r;

        r.len = max(len, a.len) + 1;

        for(register int i=0; i<r.len; i++){
            r.data[i] += (a.data[i] + data[i]);

            int x = r.data[i] / 10;

            if(x){
                r.data[i+1] += x;
                r.data[i] %= 10;
            }

        }

        while(r.data[r.len-1] == 0 && r.len > 1){
            r.len--;
        }

        return r;
    }


    bigNum operator - (bigNum const a){
        bigNum r;

        r.len = max(len, a.len);

        for(register int i=0; i<r.len; i++){
            r.data[i] += data[i] - a.data[i];

            while(r.data[i] < 0){
                r.data[i] += 10;
                r.data[i+1] --;
            }
        }

        while(r.data[r.len-1] == 0 && r.len > 1){
            r.len--;
        }

        return r;       
    }

    bigNum operator * (bigNum const a){
        bigNum r;
        r.len = a.len + len;

        for(register int i=0; i<len; i++){
            for(register int j=0; j<a.len; j++){
                int k = i + j;

                r.data[k] += data[i] * a.data[j];

                int x = r.data[k] / 10;

                if(x){
                    r.data[k+1] += x;
                    r.data[k] %= 10;
                }
            }
        }

        while(r.data[r.len-1] == 0 && r.len > 1){
            r.len--;
        }

        return r;
    }

    void operator += (bigNum const a){
        *this = (*this) + a;
    }

    void operator -= (bigNum const a){
        *this = (*this) - a;
    }   

    void operator *= (bigNum const a){
        *this = (*this) * a;
    }

};

int n;

bigNum f[MAXN*3][MAXN*3];
bigNum data[MAXN*3];
bigNum ans;

char input[SIZE];

int main(){
    scanf("%d", &n);

    for(register int i=1; i<=n; i++){
        scanf("%s", input);
        data[i + n] = data[i] = input;
    }

    for(register int i=1; i<=2*n; i++){
        for(register int j=1; j<=2*n; j++){
            f[i][j].len = 35;

            for(register int k=0; k<35; k++){
                f[i][j].data[k] = 9;
            }
        }
    }

    for(register int i=1; i<=n; i++){
        f[i][i].len = f[i][i+1].len = 1;
        memset(f[i][i].data, 0, sizeof(f[i][i].data));
        memset(f[i][i+1].data, 0, sizeof(f[i][i+1].data));
    }


    for(register int len=2; len <=n; len++){
        for(register int l=1; l<=2*n-len+1; l++){
            int r = l + len - 1;

            for(register int k=l+1; k<r; k++){
                f[l][r] = min(f[l][r], f[l][k] + f[k][r] + data[l] * data[r] * data[k]);
            }
        }
    }

    ans.len = 35;
    for(register int i=0; i<35; i++)
        ans.data[i] = 9;

    for(register int i=1; i<=n; i++){
        ans = min(ans, f[i][i+n-1]);
    }

    ans.print();
    return 0;
}